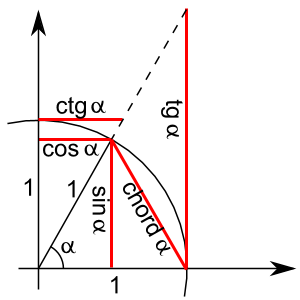Математика (Сальвеблюз)

-1 hp

Эта страница предлагается для удаления. Если вы считаете, что эту страницу не нужно удалять, выскажите ваше мнение на странице обсуждения либо данной статьи, либо участника, поставившего её на удаление, либо администратора.

Арифметика

Сложение и вычитание

Имеют геометрическое (суммарная длина двух отрезков равна длине отрезка, полученного состыковыванием исходных двух) и экономическое определение (сумма чисел имеет столько условных единиц (монет), сколько их содержится во всех слагаемых). Отрицательные числа используются как понятие «взятия в долг».

Известны свойства коммутативности (слагаемые можно менять местами), ассоциативности (операции сложения можно производить в любом порядке), понятие нуля (ничего) и противоположного числа (иметь столько же, сколько задолжать, всё равно что ничего не иметь).

Известны числа Фибоначчи (<math>1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89</math>, каждое следующее равно сумме двух предыдущих), используемые в связи с гиматриями.

Известны формулы:

<math>1+2+3+\cdots+n=\frac{n^2}2+\frac n2</math> <math>1^2+2^2+3^2+\cdots+n^2=\frac{n^3}3+\frac{n^2}2+\frac n6</math> <math>1^3+2^3+3^3+\cdots+n^3=\frac{n^4}4+\frac{n^3}2+\frac{n^2}4</math>

При этом ни общая формула, ни числа Бернулли, конечно, неизвестны. Неизвестна и символьная запись чисел (n в приведенных формулах). Одной из известных (нерешенных) задач является попытка найти столь же удобную формулу для факториала. Формулы Стирлинга нет, потому что нет экспонент.

Умножение и деление

Умножение имеет геометрическое (площадь прямоугольника или параллелепипеда) и экономическое (общий капитал, если каждый вносит определенную сумму) определения. Деление — только экономическое (сколько достанется каждому, если такую-то сумму разделить на всех поровну) в связи с трудностью практического построения фигуры заданной площади.

Произведение отрицательных чисел не определено. На практике для вычисления произведений используются таблицы простых случаев (таблица умножения, таблица Пифагора, ведический квадрат), основные правила при умножении на часто встречающиеся числа (например, основу, считаем, что 10), а также логарифмические таблицы вроде этой:

0	1	2	3	4	5	6	7	8	9	10	<math>\cdots</math>
1	2	4	8	16	32	64	128	256	512	1024	<math>\cdots</math>

Тогда, например, при умножении 16 на 32 вместо этого складываются 4 и 5, а потом совершается возврат с 9 в нижнюю строчку. Сведение произвольных чисел к табличным осуществляется, конечно, сложением.

Известны свойства коммутативности (множители можно менять местами), ассоциативности (порядок умножения не оказывает влияние на результат), дистрибутивности (произведение суммы равно сумме произведений) и понятие единицы (обычно путём унификации со считающим, то есть вместо «двое вносят по 50 монет, составляя вместе 100» говорят «я внес 50 монет, и всего получилось 50»). Известны конечные дроби и алгоритм Евклида для целых чисел.

Имеются также зачатки теории вероятностей, произошедшие из попыток решения азартных игр. Классическое определение вероятности по Лапласу как выбор из нескольких равновероятных результатов (бросок кубика, вытаскивание карты), статистическое определение как вывод из множества опытов.

Квадрат и корень

Ошибка создания миниатюры: Error: Unable to access jarfile /var/www/wikiverse/w/extensions/batik-1.7/batik-rasterizer.jar

Алгоритм, определяющий квадратный корень

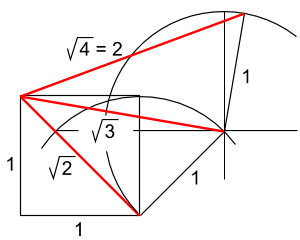
Квадрат определяется как произведение числа на самое себя или как площадь квадрата, корень из двух — как диагональ квадрата, последующие корни следующим простеньким алгоритмом с помощью циркуля и линейки.

Все числа делят на квадратные и упорствующие, для первых значение корня известно, для вторых считается итеративно по формуле: если r — текущее приближение, то следующее приближение равно <math>\frac1r+\frac r2</math> (фактически, это начало ряда Тейлора для <math>\sqrt{1+x}</math>). Третья степень (куб и не только) известна, её стереометрический смысл — тоже, степени выше могут использоваться в вычислениях, но на практике стараются не вылезать за третью степень.

Геометрия

Формы

Квадрат, прямоугольник, параллелепипед, треугольник, трапеция, шестиугольник, круг. Парабола (считается равной цепной линии), эллипс. Геометрическая единица измерения обычно называется «шагом».

Площади

Известны формулы для площадей прямоугольника и параллелепипеда (произведение основания и высоты), круга (произведение квадрата радиуса на число <math>\pi</math>), параболы (треть от двойного произведения ширины на высоту), треугольника (половина произведения основания на высоту) и трапеции (половина произведения суммы оснований на высоту). Есть и геометрическое определение вероятности как отношение площадей, известно, что его не всегда можно свести к классической (иррациональную площадь нельзя поделить на участки).

Уравнения

Геометрически находятся положительные корни квадратных уравнений (путём сложения и вычитания площадей, как у Мухаммеда ибн-Муса аль-Хварезми). Интерполяция в зачаточном виде: проведение прямой линии по двум точкам (частный случай формулы Ньютона).

Тригонометрия

Ошибка создания миниатюры: Error: Unable to access jarfile /var/www/wikiverse/w/extensions/batik-1.7/batik-rasterizer.jar

Определения тригонометрических функций

Можно рассматривать и как геометрию, и как теорию периодических функций. Положительные углы «отсчитываются вверх», отрицательные, соответственно, «вниз». Существуют пять тригонометрических функций: синус, косинус, тангенс, котангенс и хорда Птолемея.

Известны формулы как тригонометрических функций суммы и разности, так и сумм и разностей тригонометрических функций. Известно также, что при маленьких углах синус почти сходится с хордой, а при углах, близких к развернутому, косинус почти сходится с половиной хорды. Различие между длиной дуги единичной окружности и углом, которое у нас возникло из-за различных систем, не делается. Известны обратные тригонометрические функции, определяющиеся также геометрически. Из построения аркхорды непосредственно следует метод дихотомии отрезка циркулем и линейкой.

Лучшее приближение для числа пи (отношение длины окружности к её диаметру) таково:

<math>3\frac{10}{71} < \pi < 3\frac17</math>

Числовая магия

Числовой маг — это нечто среднее между математиком в древнем понимании (Пифагор, Никомед, Диоклес, Птолемей, Архимед, Евклид, Региомонтан, аль-Хорезми, Омар Хайям и пр.) и магом в историческом, но неалхимическом понимании (магические квадраты, магические формулы, нумерология, астрология, каббала, гиматрии, гексаграммы, триграммы и т.п) при условии, что вся эта штука действительно существует и работает. Числовыми магами становятся люди (самые скучные и усидчивые из них) и гномы, всем прочим расам чего-то для этого не хватает.

В период ученичества каждый числовой маг вручную переписывает особенную Книгу Чисел, которая содержит основные чертежи, формулы, теоремы и таблицы, которые будут помогать ему всю жизнь. На именном (девятом) уровне она дополняется копией Единой Книги Порядка, её более мистическим аналогом, описывающем общие принципы мироздания (то есть уже не математика как таковая, а скорее ближе к конфуцианскому У-Цзин). Также на именном уровне у числового мага появляется свой личный знак — некое подобие вензеля со всякими геометрическими наворотами. Он вносится в Единую Книгу Порядка как флазий — хранитель порядка. Этот вензель можно вплетать в любой другой знак, используемый в ритуале или заклинании — это даёт штраф к спасброску, но позволяет и безошибочно легко определить личность создавшего знак.

Магия чисел отрицает всякую хаотичность и непредсказуемость, чем противопоставляет себя дикой псионике и религии, да и вообще принципу Гейзенберга и теории хаоса (развитие науки на описанном этапе это не тормозит, то есть последствия только в отыгрыше). Считается, что числовым магам покровительствует Эврименид, но это не обязательный всеобщий закон, а всего лишь тенденция.

Ритуальная часть

Любые сложные расчёты проводятся по тем же правилам, что любая ритуальная магия. Например, проведение оценки того, сколько с города должно быть собрано налогов, если налог фиксирован и не выражается в процентах, сводится к подсчёту суммы нескольких произведений довольно больших чисел, и каждое из этих произведений раскладывается на длинный ряд сложений с использованием логарифмических таблиц, таблицы Пифагора и, возможно, каких-то специализированных вспомогательных таблиц. Всё это помимо знания самого процесса требует кучи времени, внимания, предельной аккуратности и больших запасов бумаги и чернил даже для таких «простых» случаев, не говоря уже о более сложных — скажем, рассчитать габариты и форму корабля по заданному водоизмещению или определить минимальную толщину колонн по чертежу здания. Никакая другая магия такие задачи напрямую не решает.

Ритуалы числовых магов, относящиеся к магической школе Геометрии, но не являющиеся обычными расчётами, включают, например, охранные заклинания (alarm, aerial alarm, improved alarm, glyph of warding, guards and wards, death ward, Tobian’s ultimate circle) и наложение всевозможных знаков и меток (explosive runes и sepia snake sigil, но совсем не обязательно force, moon rune, mark of water/air/earth/fire/frost, greater mark of water/air/earth/fire/frost, Jaggar’s strengthened bastion, mark of death, moonglow symbol), а также построение кругов (magic circle against …, circle of death, teleportation circle).

В отличие от школы Осуждения, числовые маги ограничены чётко знаковой магией — не могут, скажем, дать защиту от огня напрямую, а должны или рисовать соответствующий круг вокруг получателя, или метку на этом получателе. С последним вариантом они слегка забираются на вотчину алхимиков, особенно если учитывать, что могут делать постоянные метки — татуировки. Однако если у алхимиков может быть способность вида «дать оружию любое свойство ценой +1», то у числовых магов следует скорее ожидать «дать частичную защиту от огня доспехам, щиту, шлему, плащу, человеку и чему-нибудь ещё».

Боевая геометрия

Из быстрых заклинаний у числовых магов есть две категории. Первая — спонтанная демонстрация тех же символов (symbol of death/fear/insanity/pain/persuasion/sleep/stunning/weakness, symbol of thirst, symbol of spell loss) и их стирание, выключение или перенос (transcribe symbol). Вторая — «реалистичные прорицания», то есть заклинания, дающие ответы на такие вопросы, трудность которых только в отсутствии времени или инструментов для проведения расчётов: числовой маг может быть идеальным компасом (due north), картографом (Muirara’s map), стенографом (dictation, diary), художником (Prismal’s pictograph) и т. п.